Earth's magnetic field

Computer simulation of Earth's field in a period of normal polarity between reversals. The lines represent magnetic field lines, blue when the field points towards the center and yellow when away. The rotation axis of Earth is centered and vertical. The dense clusters of lines are within Earth's core.

Earth's magnetic field, also known as the geomagnetic field, is the magnetic field that extends from Earth's interior out into space, where it interacts with the solar wind, a stream of charged particles emanating from the Sun. The magnetic field is generated by electric currents due to the motion of convection currents of a mixture of molten iron and nickel in Earth's outer core: these convection currents are caused by heat escaping from the core, a natural process called a geodynamo.

The magnitude of Earth's magnetic field at its surface ranges from 25 to 65 μT (0.25 to 0.65 G). As an approximation, it is represented by a field of a magnetic dipole currently tilted at an angle of about 11° with respect to Earth's rotational axis, as if there were an enormous bar magnet placed at that angle through the center of Earth. The North geomagnetic pole (Ellesmere Island, Nunavut, Canada) actually represents the South pole of Earth's magnetic field, and conversely the South geomagnetic pole corresponds to the north pole of Earth's magnetic field (because opposite magnetic poles attract and the north end of a magnet, like a compass needle, points toward Earth's South magnetic field.)

While the North and South magnetic poles are usually located near the geographic poles, they slowly and continuously move over geological time scales, but sufficiently slowly for ordinary compasses to remain useful for navigation. However, at irregular intervals averaging several hundred thousand years, Earth's field reverses and the North and South Magnetic Poles abruptly switch places. These reversals of the geomagnetic poles leave a record in rocks that are of value to paleomagnetists in calculating geomagnetic fields in the past. Such information in turn is helpful in studying the motions of continents and ocean floors. The magnetosphere is defined by the extent of Earth's magnetic field in space or geospace. It extends above the ionosphere, several tens of thousands of kilometres into space, protecting Earth from the charged particles of the solar wind and cosmic rays that would otherwise strip away the upper atmosphere, including the ozone layer that protects Earth from harmful ultraviolet radiation.

Significance

Earth's magnetic field deflects most of the solar wind, whose charged particles would otherwise strip away the ozone layer that protects the Earth from harmful ultraviolet radiation. One stripping mechanism is for gas to be caught in bubbles of the magnetic field, which are ripped off by solar winds. Calculations of the loss of carbon dioxide from the atmosphere of Mars, resulting from scavenging of ions by the solar wind, indicate that the dissipation of the magnetic field of Mars caused a near total loss of its atmosphere.

The study of the past magnetic field of the Earth is known as paleomagnetism. The polarity of the Earth's magnetic field is recorded in igneous rocks, and reversals of the field are thus detectable as "stripes" centered on mid-ocean ridges where the sea floor is spreading, while the stability of the geomagnetic poles between reversals has allowed paleomagnetism to track the past motion of continents. Reversals also provide the basis for magnetostratigraphy, a way of dating rocks and sediments. The field also magnetizes the crust, and magnetic anomalies can be used to search for deposits of metal ores.

Humans have used compasses for direction finding since the 11th century A.D. and for navigation since the 12th century. Although the magnetic declination does shift with time, this wandering is slow enough that a simple compass can remain useful for navigation. Using magnetoreception, various other organisms, ranging from some types of bacteria to pigeons, use the Earth's magnetic field for orientation and navigation.

Characteristics

At any location, the Earth's magnetic field can be represented by a three-dimensional vector. A typical procedure for measuring its direction is to use a compass to determine the direction of magnetic North. Its angle relative to true North is the declination (D) or variation. Facing magnetic North, the angle the field makes with the horizontal is the inclination (I) or magnetic dip. The intensity (F) of the field is proportional to the force it exerts on a magnet. Another common representation is in X (North), Y (East) and Z (Down) coordinates.

Common coordinate systems used for representing the Earth's magnetic field

Intensity

The intensity of the field is often measured in gauss (G), but is generally reported in microteslas (μT), with 1 G = 100 μT. A nanotesla is also referred to as a gamma (γ). The Earth's field ranges between approximately 22 and 67 μT (0.22 and 0.67 G). By comparison, a strong refrigerator magnet has a field of about 10,000 μT (100 G).

A map of intensity contours is called an isodynamic chart. As the World Magnetic Model shows, the intensity tends to decrease from the poles to the equator. A minimum intensity occurs in the South Atlantic Anomaly over South America while there are maxima over northern Canada, Siberia, and the coast of Antarctica south of Australia.

The intensity of the magnetic field is subject to change over time. A 2021 paleomagnetic study from the University of Liverpool contributed to a growing body of evidence that the Earth's magnetic field cycles with intensity every 200 million years. The lead author stated that "Our findings, when considered alongside the existing datasets, support the existence of an approximately 200-million-year-long cycle in the strength of the Earth's magnetic field related to deep Earth processes."

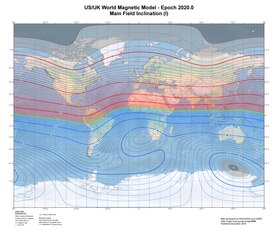
Inclination

Main article: Magnetic dip

The inclination is given by an angle that can assume values between −90° (up) to 90° (down). In the northern hemisphere, the field points downwards. It is straight down at the North Magnetic Pole and rotates upwards as the latitude decreases until it is horizontal (0°) at the magnetic equator. It continues to rotate upwards until it is straight up at the South Magnetic Pole. Inclination can be measured with a dip circle.

An isoclinic chart (map of inclination contours) for the Earth's magnetic field is shown below.

Declination

Main article: Magnetic declination

Declination is positive for an eastward deviation of the field relative to true north. It can be estimated by comparing the magnetic north–south heading on a compass with the direction of a celestial pole. Maps typically include information on the declination as an angle or a small diagram showing the relationship between magnetic north and true north. Information on declination for a region can be represented by a chart with isogonic lines (contour lines with each line representing a fixed declination).

Geographical variation

Components of the Earth's magnetic field at the surface from the World Magnetic Model for 2020.

• 
  Intensity
• 
  Inclination
• 
  Declination

Dipolar approximation

Relationship between Earth's poles. A1 and A2 are the geographic poles; B1 and B2 are the geomagnetic poles; C1 (south) and C2 (north) are the magnetic poles.

See also: Dipole model of the Earth's magnetic field

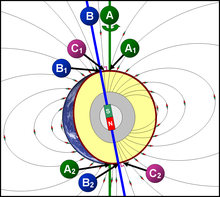
Near the surface of the Earth, its magnetic field can be closely approximated by the field of a magnetic dipole positioned at the center of the Earth and tilted at an angle of about 11° with respect to the rotational axis of the Earth. The dipole is roughly equivalent to a powerful bar magnet, with its south pole pointing towards the geomagnetic North Pole. This may seem surprising, but the north pole of a magnet is so defined because, if allowed to rotate freely, it points roughly northward (in the geographic sense). Since the north pole of a magnet attracts the south poles of other magnets and repels the north poles, it must be attracted to the south pole of Earth's magnet. The dipolar field accounts for 80–90% of the field in most locations.

Magnetic poles

Main article: Geomagnetic pole

The movement of Earth's North Magnetic Pole across the Canadian arctic

Historically, the north and south poles of a magnet were first defined by the Earth's magnetic field, not vice versa, since one of the first uses for a magnet was as a compass needle. A magnet's North pole is defined as the pole that is attracted by the Earth's North Magnetic Pole, in the arctic region, when the magnet is suspended so it can turn freely. Since opposite poles attract, the North Magnetic Pole of the Earth is really the south pole of its magnetic field (the place where the field is directed downward into the Earth).

The positions of the magnetic poles can be defined in at least two ways: locally or globally. The local definition is the point where the magnetic field is vertical. This can be determined by measuring the inclination. The inclination of the Earth's field is 90° (downwards) at the North Magnetic Pole and –90° (upwards) at the South Magnetic Pole. The two poles wander independently of each other and are not directly opposite each other on the globe. Movements of up to 40 kilometres (25 mi) per year have been observed for the North Magnetic Pole. Over the last 180 years, the North Magnetic Pole has been migrating northwestward, from Cape Adelaide in the Boothia Peninsula in 1831 to 600 kilometres (370 mi) from Resolute Bay in 2001. The magnetic equator is the line where the inclination is zero (the magnetic field is horizontal).

The global definition of the Earth's field is based on a mathematical model. If a line is drawn through the center of the Earth, parallel to the moment of the best-fitting magnetic dipole, the two positions where it intersects the Earth's surface are called the North and South geomagnetic poles. If the Earth's magnetic field were perfectly dipolar, the geomagnetic poles and magnetic dip poles would coincide and compasses would point towards them. However, the Earth's field has a significant non-dipolar contribution, so the poles do not coincide and compasses do not generally point at either.

Magnetosphere

See also: Magnetosphere

An artist's rendering of the structure of a magnetosphere. 1) Bow shock. 2) Magnetosheath. 3) Magnetopause. 4) Magnetosphere. 5) Northern tail lobe. 6) Southern tail lobe. 7) Plasmasphere.

Earth's magnetic field, predominantly dipolar at its surface, is distorted further out by the solar wind. This is a stream of charged particles leaving the Sun's corona and accelerating to a speed of 200 to 1000 kilometres per second. They carry with them a magnetic field, the interplanetary magnetic field (IMF).

The solar wind exerts a pressure, and if it could reach Earth's atmosphere it would erode it. However, it is kept away by the pressure of the Earth's magnetic field. The magnetopause, the area where the pressures balance, is the boundary of the magnetosphere. Despite its name, the magnetosphere is asymmetric, with the sunward side being about 10 Earth radii out but the other side stretching out in a magnetotail that extends beyond 200 Earth radii. Sunward of the magnetopause is the bow shock, the area where the solar wind slows abruptly.

Inside the magnetosphere is the plasmasphere, a donut-shaped region containing low-energy charged particles, or plasma. This region begins at a height of 60 km, extends up to 3 or 4 Earth radii, and includes the ionosphere. This region rotates with the Earth. There are also two concentric tire-shaped regions, called the Van Allen radiation belts, with high-energy ions (energies from 0.1 to 10 MeV). The inner belt is 1–2 Earth radii out while the outer belt is at 4–7 Earth radii. The plasmasphere and Van Allen belts have partial overlap, with the extent of overlap varying greatly with solar activity.

As well as deflecting the solar wind, the Earth's magnetic field deflects cosmic rays, high-energy charged particles that are mostly from outside the Solar System. Many cosmic rays are kept out of the Solar System by the Sun's magnetosphere, or heliosphere. By contrast, astronauts on the Moon risk exposure to radiation. Anyone who had been on the Moon's surface during a particularly violent solar eruption in 2005 would have received a lethal dose.

Some of the charged particles do get into the magnetosphere. These spiral around field lines, bouncing back and forth between the poles several times per second. In addition, positive ions slowly drift westward and negative ions drift eastward, giving rise to a ring current. This current reduces the magnetic field at the Earth's surface. Particles that penetrate the ionosphere and collide with the atoms there give rise to the lights of the aurorae while also emitting X-rays.

The varying conditions in the magnetosphere, known as space weather, are largely driven by solar activity. If the solar wind is weak, the magnetosphere expands; while if it is strong, it compresses the magnetosphere and more of it gets in. Periods of particularly intense activity, called geomagnetic storms, can occur when a coronal mass ejection erupts above the Sun and sends a shock wave through the Solar System. Such a wave can take just two days to reach the Earth. Geomagnetic storms can cause a lot of disruption; the "Halloween" storm of 2003 damaged more than a third of NASA's satellites. The largest documented storm, the Carrington Event, occurred in 1859. It induced currents strong enough to disrupt telegraph lines, and aurorae were reported as far south as Hawaii.

Time dependence

Short-term variations

Background: a set of traces from magnetic observatories showing a magnetic storm in 2000.
Globe: map showing locations of observatories and contour lines giving horizontal magnetic intensity in μ T.

The geomagnetic field changes on time scales from milliseconds to millions of years. Shorter time scales mostly arise from currents in the ionosphere (ionospheric dynamo region) and magnetosphere, and some changes can be traced to geomagnetic storms or daily variations in currents. Changes over time scales of a year or more mostly reflect changes in the Earth's interior, particularly the iron-rich core.

Frequently, the Earth's magnetosphere is hit by solar flares causing geomagnetic storms, provoking displays of aurorae. The short-term instability of the magnetic field is measured with the K-index.

Data from THEMIS show that the magnetic field, which interacts with the solar wind, is reduced when the magnetic orientation is aligned between Sun and Earth – opposite to the previous hypothesis. During forthcoming solar storms, this could result in blackouts and disruptions in artificial satellites.

Secular variation

Main article: Geomagnetic secular variation

Estimated declination contours by year, 1590 to 1990 (click to see variation)

Strength of the axial dipole component of Earth's magnetic field from 1600 to 2020

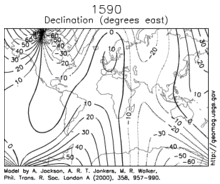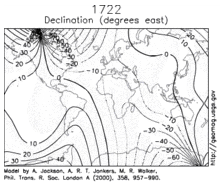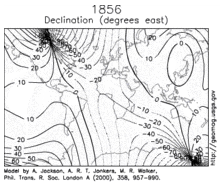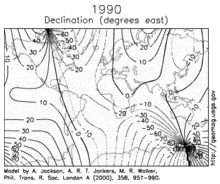
Changes in Earth's magnetic field on a time scale of a year or more are referred to as secular variation. Over hundreds of years, magnetic declination is observed to vary over tens of degrees. The animation shows how global declinations have changed over the last few centuries.

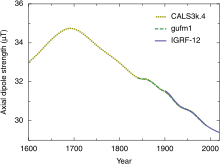
The direction and intensity of the dipole change over time. Over the last two centuries the dipole strength has been decreasing at a rate of about 6.3% per century. At this rate of decrease, the field would be negligible in about 1600 years. However, this strength is about average for the last 7 thousand years, and the current rate of change is not unusual.

A prominent feature in the non-dipolar part of the secular variation is a westward drift at a rate of about 0.2° per year. This drift is not the same everywhere and has varied over time. The globally averaged drift has been westward since about 1400 AD but eastward between about 1000 AD and 1400 AD.

Changes that predate magnetic observatories are recorded in archaeological and geological materials. Such changes are referred to as paleomagnetic secular variation or paleosecular variation (PSV). The records typically include long periods of small change with occasional large changes reflecting geomagnetic excursions and reversals.

A 1995 study of lava flows on Steens Mountain, Oregon appeared to suggest the magnetic field once shifted at a rate of up to 6° per day at some time in Earth's history, a surprising result. However, in 2014 one of the original authors published a new study which found the results were actually due to the continuous thermal demagnitization of the lava, not to a shift in the magnetic field.

In July 2020 scientists report that analysis of simulations and a recent observational field model show that maximum rates of directional change of Earth's magnetic field reached ~10° per year – almost 100 times faster than current changes and 10 times faster than previously thought.

Magnetic field reversals

Geomagnetic polarity during the late Cenozoic Era. Dark areas denote periods where the polarity matches today's polarity, light areas denote periods where that polarity is reversed.

Main article: Geomagnetic reversal

Although generally Earth's field is approximately dipolar, with an axis that is nearly aligned with the rotational axis, occasionally the North and South geomagnetic poles trade places. Evidence for these geomagnetic reversals can be found in basalts, sediment cores taken from the ocean floors, and seafloor magnetic anomalies. Reversals occur nearly randomly in time, with intervals between reversals ranging from less than 0.1 million years to as much as 50 million years. The most recent geomagnetic reversal, called the Brunhes–Matuyama reversal, occurred about 780,000 years ago. A related phenomenon, a geomagnetic excursion, takes the dipole axis across the equator and then back to the original polarity. The Laschamp event is an example of an excursion, occurring during the last ice age (41,000 years ago).

The past magnetic field is recorded mostly by strongly magnetic minerals, particularly iron oxides such as magnetite, that can carry a permanent magnetic moment. This remanent magnetization, or remanence, can be acquired in more than one way. In lava flows, the direction of the field is "frozen" in small minerals as they cool, giving rise to a thermoremanent magnetization. In sediments, the orientation of magnetic particles acquires a slight bias towards the magnetic field as they are deposited on an ocean floor or lake bottom. This is called detrital remanent magnetization.

Thermoremanent magnetization is the main source of the magnetic anomalies around mid-ocean ridges. As the seafloor spreads, magma wells up from the mantle, cools to form new basaltic crust on both sides of the ridge, and is carried away from it by seafloor spreading. As it cools, it records the direction of the Earth's field. When the Earth's field reverses, new basalt records the reversed direction. The result is a series of stripes that are symmetric about the ridge. A ship towing a magnetometer on the surface of the ocean can detect these stripes and infer the age of the ocean floor below. This provides information on the rate at which seafloor has spread in the past.

Radiometric dating of lava flows has been used to establish a geomagnetic polarity time scale, part of which is shown in the image. This forms the basis of magnetostratigraphy, a geophysical correlation technique that can be used to date both sedimentary and volcanic sequences as well as the seafloor magnetic anomalies.

Earliest appearance

Paleomagnetic studies of Paleoarchean lava in Australia and conglomerate in South Africa have concluded that the magnetic field has been present since at least about 3,450 million years ago. In 2024 researchers published evidence from Greenland for the existence of the magnetic field as early as 3,700 million years ago.

Future

Variations in virtual axial dipole moment since the last reversal

Starting in the late 1800s and throughout the 1900s and later, the overall geomagnetic field has become weaker; the present strong deterioration corresponds to a 10–15% decline and has accelerated since 2000; geomagnetic intensity has declined almost continuously from a maximum 35% above the modern value, from circa year 1 AD. The rate of decrease and the current strength are within the normal range of variation, as shown by the record of past magnetic fields recorded in rocks.

The nature of Earth's magnetic field is one of heteroscedastic (seemingly random) fluctuation. An instantaneous measurement of it, or several measurements of it across the span of decades or centuries, are not sufficient to extrapolate an overall trend in the field strength. It has gone up and down in the past for unknown reasons. Also, noting the local intensity of the dipole field (or its fluctuation) is insufficient to characterize Earth's magnetic field as a whole, as it is not strictly a dipole field. The dipole component of Earth's field can diminish even while the total magnetic field remains the same or increases.

The Earth's magnetic north pole is drifting from northern Canada towards Siberia with a presently accelerating rate—10 kilometres (6.2 mi) per year at the beginning of the 1900s, up to 40 kilometres (25 mi) per year in 2003, and since then has only accelerated.

Physical origin

Main article: Dynamo theory

Earth's core and the geodynamo

The Earth's magnetic field is believed to be generated by electric currents in the conductive iron alloys of its core, created by convection currents due to heat escaping from the core.

A schematic illustrating the relationship between motion of conducting fluid, organized into rolls by the Coriolis force, and the magnetic field the motion generates.

The Earth and most of the planets in the Solar System, as well as the Sun and other stars, all generate magnetic fields through the motion of electrically conducting fluids. The Earth's field originates in its core. This is a region of iron alloys extending to about 3400 km (the radius of the Earth is 6370 km). It is divided into a solid inner core, with a radius of 1220 km, and a liquid outer core. The motion of the liquid in the outer core is driven by heat flow from the inner core, which is about 6,000 K (5,730 °C; 10,340 °F), to the core-mantle boundary, which is about 3,800 K (3,530 °C; 6,380 °F). The heat is generated by potential energy released by heavier materials sinking toward the core (planetary differentiation, the iron catastrophe) as well as decay of radioactive elements in the interior. The pattern of flow is organized by the rotation of the Earth and the presence of the solid inner core.

The mechanism by which the Earth generates a magnetic field is known as a geodynamo. The magnetic field is generated by a feedback loop: current loops generate magnetic fields (Ampère's circuital law); a changing magnetic field generates an electric field (Faraday's law); and the electric and magnetic fields exert a force on the charges that are flowing in currents (the Lorentz force). These effects can be combined in a partial differential equation for the magnetic field called the magnetic induction equation,

${\frac {\partial \mathbf {B} }{\partial t}}=\eta \nabla ^{2}\mathbf {B} +\nabla \times (\mathbf {u} \times \mathbf {B} ),$

where u is the velocity of the fluid; B is the magnetic B-field; and η = 1/σμ is the magnetic diffusivity, which is the reciprocal of the product of the electrical conductivity σ and the permeability μ . The term ∂B/∂t is the partial derivative of the field with respect to time; ∇² is the Laplace operator, ∇× is the curl operator, and × is the vector product.

The first term on the right hand side of the induction equation is a diffusion term. In a stationary fluid, the magnetic field declines and any concentrations of field spread out. If the Earth's dynamo shut off, the dipole part would disappear in a few tens of thousands of years.

In a perfect conductor ($\sigma =\infty \;$), there would be no diffusion. By Lenz's law, any change in the magnetic field would be immediately opposed by currents, so the flux through a given volume of fluid could not change. As the fluid moved, the magnetic field would go with it. The theorem describing this effect is called the frozen-in-field theorem. Even in a fluid with a finite conductivity, new field is generated by stretching field lines as the fluid moves in ways that deform it. This process could go on generating new field indefinitely, were it not that as the magnetic field increases in strength, it resists fluid motion.

The motion of the fluid is sustained by convection, motion driven by buoyancy. The temperature increases towards the center of the Earth, and the higher temperature of the fluid lower down makes it buoyant. This buoyancy is enhanced by chemical separation: As the core cools, some of the molten iron solidifies and is plated to the inner core. In the process, lighter elements are left behind in the fluid, making it lighter. This is called compositional convection. A Coriolis effect, caused by the overall planetary rotation, tends to organize the flow into rolls aligned along the north–south polar axis.

A dynamo can amplify a magnetic field, but it needs a "seed" field to get it started. For the Earth, this could have been an external magnetic field. Early in its history the Sun went through a T-Tauri phase in which the solar wind would have had a magnetic field orders of magnitude larger than the present solar wind. However, much of the field may have been screened out by the Earth's mantle. An alternative source is currents in the core-mantle boundary driven by chemical reactions or variations in thermal or electric conductivity. Such effects may still provide a small bias that are part of the boundary conditions for the geodynamo.

The average magnetic field in the Earth's outer core was calculated to be 25 gauss, 50 times stronger than the field at the surface.

Numerical models

Simulating the geodynamo by computer requires numerically solving a set of nonlinear partial differential equations for the magnetohydrodynamics (MHD) of the Earth's interior. Simulation of the MHD equations is performed on a 3D grid of points and the fineness of the grid, which in part determines the realism of the solutions, is limited mainly by computer power. For decades, theorists were confined to creating kinematic dynamo computer models in which the fluid motion is chosen in advance and the effect on the magnetic field calculated. Kinematic dynamo theory was mainly a matter of trying different flow geometries and testing whether such geometries could sustain a dynamo.

The first self-consistent dynamo models, ones that determine both the fluid motions and the magnetic field, were developed by two groups in 1995, one in Japan and one in the United States. The latter received attention because it successfully reproduced some of the characteristics of the Earth's field, including geomagnetic reversals.

Effect of ocean tides

The oceans contribute to Earth's magnetic field. Seawater is an electrical conductor, and therefore interacts with the magnetic field. As the tides cycle around the ocean basins, the ocean water essentially tries to pull the geomagnetic field lines along. Because the salty water is only slightly conductive, the interaction is relatively weak: the strongest component is from the regular lunar tide that happens about twice per day (M2). Other contributions come from ocean swell, eddies, and even tsunamis.

Sea level magnetic fields observed by satellites (NASA)

The strength of the interaction depends also on the temperature of the ocean water. The entire heat stored in the ocean can now be inferred from observations of the Earth's magnetic field.

Currents in the ionosphere and magnetosphere

Electric currents induced in the ionosphere generate magnetic fields (ionospheric dynamo region). Such a field is always generated near where the atmosphere is closest to the Sun, causing daily alterations that can deflect surface magnetic fields by as much as 1°. Typical daily variations of field strength are about 25 nT (one part in 2000), with variations over a few seconds of typically around 1 nT (one part in 50,000).

Measurement and analysis

Detection

The Earth's magnetic field strength was measured by Carl Friedrich Gauss in 1832 and has been repeatedly measured since then, showing a relative decay of about 10% over the last 150 years. The Magsat satellite and later satellites have used 3-axis vector magnetometers to probe the 3-D structure of the Earth's magnetic field. The later Ørsted satellite allowed a comparison indicating a dynamic geodynamo in action that appears to be giving rise to an alternate pole under the Atlantic Ocean west of South Africa.

Governments sometimes operate units that specialize in measurement of the Earth's magnetic field. These are geomagnetic observatories, typically part of a national Geological survey, for example, the British Geological Survey's Eskdalemuir Observatory. Such observatories can measure and forecast magnetic conditions such as magnetic storms that sometimes affect communications, electric power, and other human activities.

The International Real-time Magnetic Observatory Network, with over 100 interlinked geomagnetic observatories around the world, has been recording the Earth's magnetic field since 1991.

The military determines local geomagnetic field characteristics, in order to detect anomalies in the natural background that might be caused by a significant metallic object such as a submerged submarine. Typically, these magnetic anomaly detectors are flown in aircraft like the UK's Nimrod or towed as an instrument or an array of instruments from surface ships.

Commercially, geophysical prospecting companies also use magnetic detectors to identify naturally occurring anomalies from ore bodies, such as the Kursk Magnetic Anomaly.

Crustal magnetic anomalies

Main article: Magnetic anomaly

A model of short-wavelength features of Earth's magnetic field, attributed to lithospheric anomalies

Magnetometers detect minute deviations in the Earth's magnetic field caused by iron artifacts, kilns, some types of stone structures, and even ditches and middens in archaeological geophysics. Using magnetic instruments adapted from airborne magnetic anomaly detectors developed during World War II to detect submarines, the magnetic variations across the ocean floor have been mapped. Basalt — the iron-rich, volcanic rock making up the ocean floor — contains a strongly magnetic mineral (magnetite) and can locally distort compass readings. The distortion was recognized by Icelandic mariners as early as the late 18th century. More important, because the presence of magnetite gives the basalt measurable magnetic properties, these magnetic variations have provided another means to study the deep ocean floor. When newly formed rock cools, such magnetic materials record the Earth's magnetic field.

Statistical models

Each measurement of the magnetic field is at a particular place and time. If an accurate estimate of the field at some other place and time is needed, the measurements must be converted to a model and the model used to make predictions.

Spherical harmonics

See also: Multipole expansion

Schematic representation of spherical harmonics on a sphere and their nodal lines. P_{ℓ m} is equal to 0 along m great circles passing through the poles, and along ℓ-m circles of equal latitude. The function changes sign each ℓtime it crosses one of these lines.

Example of a quadrupole field. This can also be constructed by moving two dipoles together.

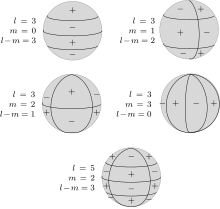
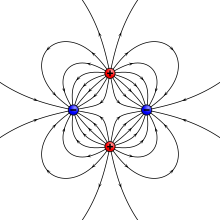
The most common way of analyzing the global variations in the Earth's magnetic field is to fit the measurements to a set of spherical harmonics. This was first done by Carl Friedrich Gauss. Spherical harmonics are functions that oscillate over the surface of a sphere. They are the product of two functions, one that depends on latitude and one on longitude. The function of longitude is zero along zero or more great circles passing through the North and South Poles; the number of such nodal lines is the absolute value of the order m. The function of latitude is zero along zero or more latitude circles; this plus the order is equal to the degree ℓ. Each harmonic is equivalent to a particular arrangement of magnetic charges at the center of the Earth. A monopole is an isolated magnetic charge, which has never been observed. A dipole is equivalent to two opposing charges brought close together and a quadrupole to two dipoles brought together. A quadrupole field is shown in the lower figure on the right.

Spherical harmonics can represent any scalar field (function of position) that satisfies certain properties. A magnetic field is a vector field, but if it is expressed in Cartesian components X, Y, Z, each component is the derivative of the same scalar function called the magnetic potential. Analyses of the Earth's magnetic field use a modified version of the usual spherical harmonics that differ by a multiplicative factor. A least-squares fit to the magnetic field measurements gives the Earth's field as the sum of spherical harmonics, each multiplied by the best-fitting Gauss coefficient g_m^ℓ or h_m^ℓ.

The lowest-degree Gauss coefficient, g₀⁰, gives the contribution of an isolated magnetic charge, so it is zero. The next three coefficients – g₁⁰, g₁¹, and h₁¹ – determine the direction and magnitude of the dipole contribution. The best fitting dipole is tilted at an angle of about 10° with respect to the rotational axis, as described earlier.

Radial dependence

Spherical harmonic analysis can be used to distinguish internal from external sources if measurements are available at more than one height (for example, ground observatories and satellites). In that case, each term with coefficient g_m^ℓ or h_m^ℓ can be split into two terms: one that decreases with radius as 1/r^ℓ+1 and one that increases with radius as r^ℓ. The increasing terms fit the external sources (currents in the ionosphere and magnetosphere). However, averaged over a few years the external contributions average to zero.

The remaining terms predict that the potential of a dipole source (ℓ=1) drops off as 1/r². The magnetic field, being a derivative of the potential, drops off as 1/r³. Quadrupole terms drop off as 1/r⁴, and higher order terms drop off increasingly rapidly with the radius. The radius of the outer core is about half of the radius of the Earth. If the field at the core-mantle boundary is fit to spherical harmonics, the dipole part is smaller by a factor of about 8 at the surface, the quadrupole part by a factor of 16, and so on. Thus, only the components with large wavelengths can be noticeable at the surface. From a variety of arguments, it is usually assumed that only terms up to degree 14 or less have their origin in the core. These have wavelengths of about 2,000 km (1,200 mi) or less. Smaller features are attributed to crustal anomalies.

Global models

The International Association of Geomagnetism and Aeronomy maintains a standard global field model called the International Geomagnetic Reference Field (IGRF). It is updated every five years. The 11th-generation model, IGRF11, was developed using data from satellites (Ørsted, CHAMP and SAC-C) and a world network of geomagnetic observatories. The spherical harmonic expansion was truncated at degree 10, with 120 coefficients, until 2000. Subsequent models are truncated at degree 13 (195 coefficients).

Another global field model, called the World Magnetic Model, is produced jointly by the United States National Centers for Environmental Information (formerly the National Geophysical Data Center) and the British Geological Survey. This model truncates at degree 12 (168 coefficients) with an approximate spatial resolution of 3,000 kilometers. It is the model used by the United States Department of Defense, the Ministry of Defence (United Kingdom), the United States Federal Aviation Administration (FAA), the North Atlantic Treaty Organization (NATO), and the International Hydrographic Organization as well as in many civilian navigation systems.

The above models only take into account the "main field" at the core-mantle boundary. Although generally good enough for navigation, higher-accuracy use cases require smaller-scale magnetic anomalies and other variations to be considered. Some examples are (see geomag.us ref for more):

• The "comprehensive modeling" (CM) approach by the Goddard Space Flight Center (NASA and GSFC) and the Danish Space Research Institute. CM attempts to reconcile data with greatly varying temporal and spatial resolution from ground and satellite sources. The latest version as of 2022 is CM5 of 2016. It provides separate components for main field plus lithosphere (crustal), M2 tidal, and primary/induced magnetosphere/ionosphere variations.
• The US National Centers for Environmental Information developed the Enhanced Magnetic Model (EMM), which extends to degree and order 790 and resolves magnetic anomalies down to a wavelength of 56 kilometers. It was compiled from satellite, marine, aeromagnetic and ground magnetic surveys. As of 2018, the latest version, EMM2017, includes data from The European Space Agency's Swarm satellite mission.

For historical data about the main field, the IGRF may be used back to year 1900. A specialized GUFM1 model estimates back to year 1590 using ship's logs. Paleomagnetic research has produced models dating back to 10,000 BCE.

Biomagnetism

Main article: Magnetoreception

Animals, including birds and turtles, can detect the Earth's magnetic field, and use the field to navigate during migration. Some researchers have found that cows and wild deer tend to align their bodies north–south while relaxing, but not when the animals are under high-voltage power lines, suggesting that magnetism is responsible. Other researchers reported in 2011 that they could not replicate those findings using different Google Earth images.

Very weak electromagnetic fields disrupt the magnetic compass used by European robins and other songbirds, which use the Earth's magnetic field to navigate. Neither power lines nor cellphone signals are to blame for the electromagnetic field effect on the birds; instead, the culprits have frequencies between 2 kHz and 5 MHz. These include AM radio signals and ordinary electronic equipment that might be found in businesses or private homes.

See also

• Polar wind
• Geomagnetic jerk
• Geomagnetic latitude
• Magnetic field of Mars
• Magnetotellurics
• Meteorite
• Operation Argus
• Rings of Saturn
• South Atlantic Anomaly

Sources

• Campbell, Wallace H. (2003). Introduction to geomagnetic fields (2nd ed.). New York: Cambridge University Press. ISBN 978-0-521-52953-2.
• Merrill, Ronald T. (2010). Our Magnetic Earth: The Science of Geomagnetism. University of Chicago Press. ISBN 978-0-226-52050-6.
• Merrill, Ronald T.; McElhinny, Michael W.; McFadden, Phillip L. (1996). The magnetic field of the earth: paleomagnetism, the core, and the deep mantle. Academic Press. ISBN 978-0-12-491246-5.
• Tauxe, Lisa (1998). Paleomagnetic Principles and Practice. Kluwer. ISBN 978-0-7923-5258-7.

Further reading

• Gramling, Carolyn (1 February 2019). "Earth's core may have hardened just in time to save its magnetic field". Science News. Retrieved 3 February 2019.
• Herndon, J. M. (1996-01-23). "Substructure of the inner core of the Earth". PNAS. 93 (2): 646–648. Bibcode:1996PNAS...93..646H. doi:10.1073/pnas.93.2.646. PMC 40105. PMID 11607625.
• Hollenbach, D. F.; Herndon, J. M. (2001-09-25). "Deep-Earth reactor: Nuclear fission, helium, and the geomagnetic field". PNAS. 98 (20): 11085–90. Bibcode:2001PNAS...9811085H. doi:10.1073/pnas.201393998. PMC 58687. PMID 11562483.
• Love, Jeffrey J. (2008). "Magnetic monitoring of Earth and space" (PDF). Physics Today. 61 (2): 31–37. Bibcode:2008PhT....61b..31H. doi:10.1063/1.2883907.
• "Temperature of the Earth's core". NEWTON Ask a Scientist. 1999. Archived from the original on 2010-09-08. Retrieved 2006-01-21.
• Towle, J. N. (1984). "The Anomalous Geomagnetic Variation Field and Geoelectric Structure Associated with the Mesa Butte Fault System, Arizona". Geological Society of America Bulletin. 9 (2): 221–225. Bibcode:1984GSAB...95..221T. doi:10.1130/0016-7606(1984)95<221:TAGVFA>2.0.CO;2.
• Turner, Gillian (2011). North Pole, South Pole: The epic quest to solve the great mystery of Earth's magnetism. New York, NY: The Experiment. ISBN 978-1-61519-031-7.
• Wait, James R. (1954). "On the relation between telluric currents and the earth's magnetic field". Geophysics. 19 (2): 281–289. Bibcode:1954Geop...19..281W. doi:10.1190/1.1437994. S2CID 51844483.
• Walt, Martin (1994). Introduction to Geomagnetically Trapped Radiation. Cambridge University Press. ISBN 978-0-521-61611-9.

External links

• Geomagnetism & Paleomagnetism background material Archived 2013-03-03 at the Wayback Machine. American Geophysical Union Geomagnetism and Paleomagnetism Section.
• National Geomagnetism Program. United States Geological Survey, March 8, 2011.
• BGS Geomagnetism. Information on monitoring and modeling the geomagnetic field. British Geological Survey, August 2005.
• William J. Broad, Will Compasses Point South?. The New York Times, July 13, 2004.
• John Roach, Why Does Earth's Magnetic Field Flip?. National Geographic, September 27, 2004.
• Magnetic Storm. PBS NOVA, 2003. (ed. about pole reversals)
• When North Goes South. Projects in Scientific Computing, 1996.
• The Great Magnet, the Earth, History of the discovery of Earth's magnetic field by David P. Stern.
• Exploration of the Earth's Magnetosphere Archived 2013-02-14 at the Wayback Machine, Educational web site by David P. Stern and Mauricio Peredo
• International Geomagnetic Reference Field 2011
• Global evolution/anomaly of the Earth's magnetic field Archived 2016-06-24 at the Wayback Machine Sweeps are in 10° steps at 10 years intervals. Based on data from: The Institute of Geophysics, ETH Zurich Archived 2007-10-31 at the Wayback Machine
• Patterns in Earth's magnetic field that evolve on the order of 1,000 years Archived 2018-07-20 at the Wayback Machine. July 19, 2017
• Chree, Charles (1911). "Magnetism, Terrestrial" . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 17 (11th ed.). Cambridge University Press. pp. 353–385. (with dozens of tables and several diagrams)